Band Pass Filter
A band-pass filter is a circuit which is designed to pass signals only in a certain band of frequencies while attenuating all signals outside this band. The parameters of importance in a bandpass filter are the high and low cut-off frequencies (fH and fl), the bandwidth (BW), the centre frequency fc, centre-frequency gain, and the selectivity or Q.
There are basically two types of bandpass filters viz wide bandpass and narrow bandpass filters. Unfortunately, there is no set dividing line between the two. However, a bandpass filter is defined as a wide bandpass if its figure of merit or quality factor Q is less than 10 while the bandpass filters with Q > 10 are called the narrow bandpass filters. Thus Q is a measure of selectivity, meaning the higher the value of Q the more selective is the filter, or the narrower is the bandwidth (BW). The relationship between Q, 3-db bandwidth, and the centre frequency fc is given by an equation
For a wide bandpass filter the centre frequency can be defined as where fH and fL are respectively the high and low cut-off frequencies in Hz.In a narrow bandpass filter, the output voltage peaks at the centre frequency fc.
Wide Bandpass Filter
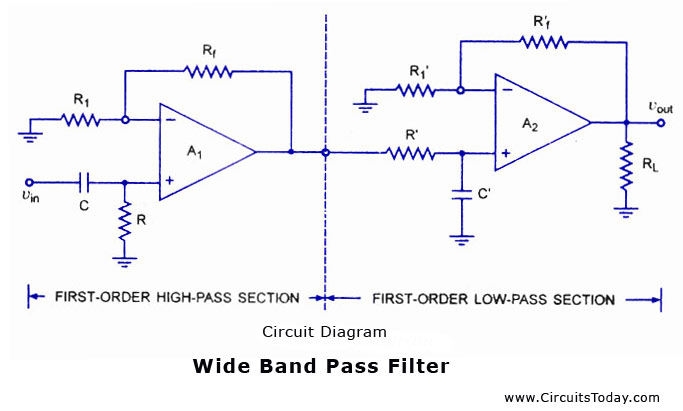
A wide bandpass filter can be formed by simply cascading high-pass and low-pass sections and is generally the choice for simplicity of design and performance though such a circuit can be realized by a number of possible circuits. To form a ± 20 db/ decade bandpass filter, a first-order high-pass and a first-order low-pass sections are cascaded; for a ± 40 db/decade bandpass filter, second-order high- pass filter and a second-order low-pass filter are connected in series, and so on. It means that, the order of the bandpass filter is governed by the order of the high-pass and low-pass filters it consists of.
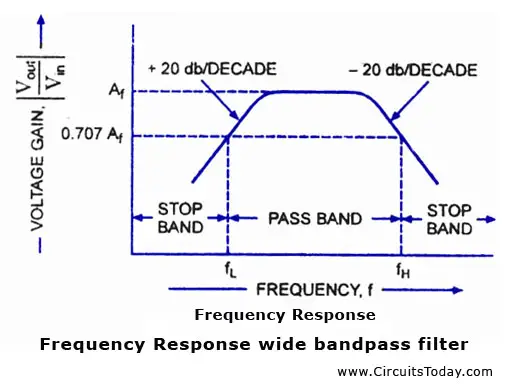
A ± 20 db/decade wide bandpass filter composed of a first-order high-pass filter and a first-order low-pass filter, is illustrated in fig. (a). Its frequency response is illustrated in fig. (b).
Narrow Bandpass Filter.
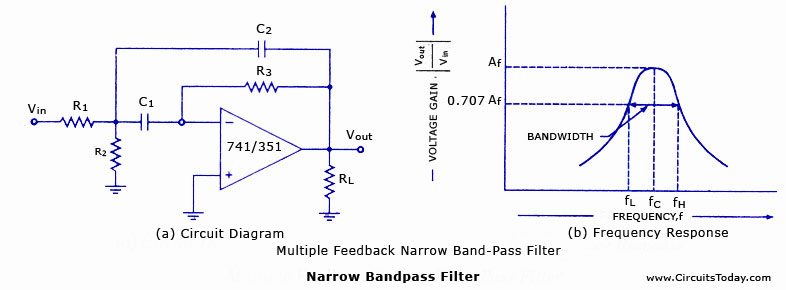
A narrow bandpass filter employing multiple feedback is depicted in figure. This filter employs only one op-amp, as shown in the figure. In comparison to all the filters discussed so far, this filter has some unique features that are given below.
1. It has two feedback paths, and this is the reason that it is called a multiple-feedback filter.
2. The op-amp is used in the inverting mode.
The frequency response of a narrow bandpass filter is shown in fig(b).
Generally, the narrow bandpass filter is designed for specific values of centre frequency fc and Q or fc and BW. The circuit components are determined from the following relationships. For simplification of design calculations each of C1 and C2 may be taken equal to C.
R1 = Q/2∏ fc CAf
R2 =Q/2∏ fc C(2Q2-Af)
and R3 = Q / ∏ fc C
where Af, is the gain at centre frequency and is given as
Af = R3 / 2R1
The gain Af however must satisfy the condition Af < 2 Q2.
The centre frequency fc of the multiple feedback filter can be changed to a new frequency fc‘ without changing, the gain or bandwidth. This is achieved simply by changing R2 to R’2 so that
R’2 = R2 [fc/f’c]2
Share this on your favourite network







Just found your post by searching on the Google, I am Impressed and Learned Lot of new thing from your post.
ReplyDeleteThank you for providing this information. Only two months ago, I was in desperate need of a band pass filters. After doing some research online, I came across the Anatech Electronics website. I received all of my required band pass filters, as well as I requested them for a custom band pass filter, and received the best quality products from them on time as like they committed. You can also reach out to them if you require any band pass filters.
ReplyDelete